Liebe Freunde der Freiheit und des Friedens,
liebe Steemians, liebe Freunde der Mathematik.
ich habe ein Problem, dass ich am Sonntag auch nach gefühlten Stunden nicht lösen konnte - zumindest nicht in einer für mich befriedigenden Art und Weise. Dieses Problem, welches der staaltiche Bildungssozialismus ohne Lösungsvorgabe dabei den Schülern auferlegt hat, wurde somit in der Folge mir aufgehalst, obwohl ich besseres und wichtigeres zu tun habe, als das die Folgen des Versagens des staatlichen Bildungswesens und seiner sozialistischen Heilsbringer fortlaufend auszubügeln.
Der Bildungsozialismus und dessen marodes und ineffizientes staatliches Bildungssystem ist für viele Missstände abseits der Schule mitverantwortliche, in dem die Bezahlung des Lehrbetriebes und der Lehrer nicht nach Erfolgsparametern definiert, sondern fortlaufend ohne Erfolgskontrolle bei den Lehrern erfolgt, egal wie mies der Unterricht in den staatlichen Bildungseinrichtungen am Ende auch sein mag.
Scheinbar gibt es Lehrer in diesem Land, die ihre Aufgaben im Sozialismus eher schlecht als recht versehen - und angesichts der fehlenden Leistungsorientierung bei den Gehaltszahlungen in Form von Lernerfolgen ihr pädagogisches Missmanagement und fehlende Erfolgsorientierung im Unterricht, den eh schon beruflich vom Sozialismus drangsalierten Eltern aufhalsen - erst recht wo in Zeiten der staatlich verordneten Verkürzung des Bildungsweges zum Abitur in 12 Jahren, die Jugend nicht nur ihrer notwendigen Freiräume zur Entwicklung ihrer Persönlichkeit beraubt werden, sondern mit zum Teil vollkommen unsinngen Lehrstoff abseits individueller Talente und Interessen abgefüllt und vor allem, so der Anschein, immer mehr vom staatlich verordneten Missmanagement in den Schulen seitens des Lehrbetriebes im Stich gelassen werden, was angesicht des hohen Zuspruchs für Onlinevideoformate für alle möglichen Lehrinhalte, den deutschen Lehrern insgesamt und dem staatlichen Bildungsbetriebin Deutschland im besonderen ein grotten schlechtes Zeugnis ausstellt, sofern man von einigen wenigen erfreulichen Ausnahmen innerhalb der Lehrerschaft mal absieht.
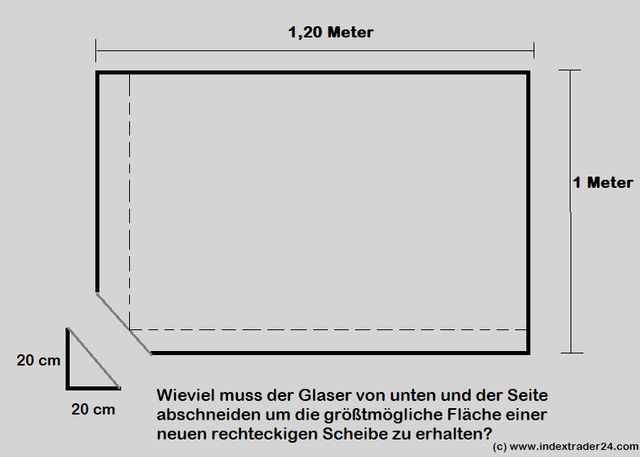
Beispielhaft sei an dieser Stelle folgende Mathematikaufgabe genannt, welche Schülern in der 9. Klasse der gymnasialen Mittelstufe zur Hausaufgabe auferlegt wurde. Die Skizze dazu kann im Eingang dieses Beitrages eingesehen werden...
Die Frage!
Es soll die größtmögliche Fläche einer rechteckigen Scheibe berechnet werden, die aus einer Scheibe herausgeschnitten werden kann bei der eine Ecke in der unten dargestellten Weise heraus gebrochen ist. Ermittle die Lösung mittels Quadratgleichungen!

Wie man eine Fläche berechnet ist mir schon klar - doch die größtmögliche Fläche in einer solchen Situation zu berechnen erfordert dann mehr als 30 Jahre nach dem Abitur doch einiges an Gehirnschmalz. Zu meinen Gymnasialzeiten hätte ich die Aufgabe sicherlich nach 15-20 Minuten gelöst. Doch heute?
Quadratische Gleichungen im Sinne von ax+bx²+c=0 und deren Umformung dämmerten mir dann aus den Tiefen meines Urzeitgedächtnis noch. Ebenso etwas wie Parabelfunktionen im Sinne von ax². Die Idee, dass im Scheitelpunkt einer Parabel die Fläche der neuen Scheibe am größten sein müsste, kam ebenso. Doch wie lässt sich eine solche in diesem Fall mathematisch umsetzen, um die Aufgabe perfekt zu lösen?
Gesucht wird demnach die neue größtmögliche Fläche A`= X * Y, die sich aus der alten Scheibe rausschneiden lässt.
Eine Überlegung war dies mittels eines Stauungsansatz zu lösen, da an der abgebrochenen Ecke jeweils 20 cm vorhanden waren - aber die Idee funzt nicht, weil das neue Rechteck dem alten nicht ähnlich ist. Also muss die Lösung komplizierter sein. Strahlensätze anzuwenden hilft ebenfalls nicht weiter.
Wenn jemand die Lösung kennt, fände ich es klasse, wenn er diese hier als Kommentar mal einstellen könnte.
Für jeden Mathematiker sicherlich eine Leichtigkeit, die zum Alltag gehört. Vermute mal, dass man irgendwie die Steigung des Dreiecks der abgebrochenen Ecke ermitteln muss und dies als Parabelfunktion mit einem Schnittpunkt sprich ax²=0 formulieren muss, um die größtmögliche Fläche - sprich den Auflagepunkt auf der verbliebenen Schräge zu berechnen.
Der Rest dürfte dann vermutlich nur wieder aus üblichen Umformerei bestehen...
Vorab schon einmal herzlichen Dank für alle Lösungsvorschläge zu diesem Matheproblem, dass mir auf Grund des Versagens des staatlichen sozialistischen staatlichen Bildungsbetriebes am Wochenende aufgehalst wurde und die Stimmung ordentlich vermieste...
Es ist eh ein Armutszeugnis für Deutschland, wenn Eltern massenhaft wegen des sozialistischen Staatsversagens bei der Bildung und dessen Ineffiziensen fortlaufend ihre Kinder zu Lernsklaven eines bolchewistischen Unrechtssystems degradiert und manche Familie zusätzlich etliche Tausender im Laufe der Zeit für Nachhilfeunterricht ausgibt - ohne dass dies Früchte trägt.
So hat ein befreundeter Vater allein in den ersten zwei Monaten des Jahres 800 Euro für Nachhilfe bei seinen beiden Kindern ausgegeben - ohne dass dies gefruchtet hätte. Ich habe ihm empfohlen, die Nachhilfe selber zu übernehmen, da ich davon ausgehe, dass diese Art der Nachhilfe von Kindern und Jugendlichen, welche unbewusst die Nähe zu ihren Eltern suchen, wahrscheinlich gar nicht gewünscht ist und auch gar nicht die Motivation am Lernen fördern wird, solange die Eltern dies nicht selber in die Hand nehmen...
Ich kann zwar vieles an Problemen abseits meines erlernten Berufes lösen, aber bei weitem nicht alles, vor allem, wenn dies aus dem Stehgreif in einem Feld erfolgen soll, in dem man sich vorher eigentlich noch mal einlesen müsste, wozu aber in Zeiten des sozialistischen Bevormundung definitiv die Zeit fehlt..
Wie dem auch sei - wer das Matheproblem hier lösen kann, bekommt auf jeden Fall schon jetzt ein fettes Danke. Ein upvote von mir und von hoffentlich ebenso vielen Lesern wird dann auch noch kommen.
Wer ist also auf Steemit der Mathepapst, der solche oder ähnliche Fragen der Abstraktion beantworten kann, so dass auch Schüler dies verstehen, denen man vorher keinen Lösungsweg gezeigt hat...
Keine Kommentare:
Kommentar veröffentlichen